抽象数据类型
与机器语言、汇编语言相比,高级语言的出现大大地简便了程序设计。但算法从非形式的自然语言表达到形式化的高级语言表达,仍然是一个复杂的过程,仍然要做很多繁杂琐碎的事情,因而仍然需要抽象。
对于一个明确的数学问题,设计它的算法,总是先选用该问题的一个数据模型。接着,弄清该问题所选用的数据模型在已知条件下的初始状态和要求的结果状态,以及隐含着的两个状态之间的关系。然后探索从数据模型的已知初始状态出发到达要求的结果状态所必需的运算步骤。把这些运算步骤记录下来,就是该问题的求解算法。
按照自顶向下逐步求精的原则,我们在探索运算步骤时,首先应该考虑算法顶层的运算步骤,然后再考虑底层的运算步骤。所谓顶层的运算步骤是指定义在数据模型级上的运算步骤,或叫宏观运算。它们组成算法的主干部分。表达这部分算法的程序就是主程序。其中涉及的数据是数据模型中的一个变量,暂时不关心它的数据结构;涉及的运算以数据模型中的数据变量作为运算对象,或作为运算结果,或二者兼而为之,简称为定义在数据模型上的运算。由于暂时不关心变量的数据结构,这些运算都带有抽象性质,不含运算的细节。所谓底层的运算步骤是指顶层抽象的运算的具体实现。它们依赖于数据模型的结构,依赖于数据模型结构的具体表示。因此,底层的运算步骤包括两部分:一是数据模型的具体表示;二是定义在该数据模型上的运算的具体实现。我们可以把它们理解为微观运算。于是,底层运算是顶层运算的细化;底层运算为顶层运算服务。为了将顶层算法与底层算法隔开,使二者在设计时不会互相牵制、互相影响,必须对二者的接口进行一次抽象。让底层只通过这个接口为顶层服务,顶层也只通过这个接口调用底层的运算。这个接口就是抽象数据类型。其英文术语是Abstract Data Types,简记ADT。
抽象数据类型是算法设计和程序设计中的重要概念。严格地说,它是算法的一个数据模型连同定义在该模型上、作为该算法构件的一组运算。这个概念明确地把数据模型与作用在该模型上的运算紧密地联系起来。事实正是如此。一方面,如前面指出过的,数据模型上的运算依赖于数据模型的具体表示,因为数据模型上的运算以数据模型中的数据变量作为运算对象,或作为运算结果,或二者兼而为之;另方面,有了数据模型的具体表示,有了数据模型上运算的具体实现,运算的效率随之确定。于是,就有这样的一个问题:如何选择数据模型的具体表示使该模型上的各种运算的效率都尽可能地高?很明显,对于不同的运算组,为使组中所有运算的效率都尽可能地高,其相应的数据模型具体表示的选择将是不同的。在这个意义下,数据模型的具体表示又反过来依赖于数据模型上定义的那些运算。特别是,当不同运算的效率互相制约时,还必须事先将所有的运算的相应使用频度排序,让所选择的数据模型的具体表示优先保证使用频度较高的运算有较高的效率。数据模型与定义在该模型上的运算之间存在着的这种密不可分的联系,是抽象数据类型的概念产生的背景和依据。
应该指出,抽象数据类型的概念并不是全新的概念。它实际上是我们熟悉的基本数据类型概念的引伸和发展。用过高级语言进行算法设计和程序设计的人都知道,基本数据类型已隐含着数据模型和定义在该模型上的运算的统一,只是当时还没有形成抽象数据类型的概念罢了。事实上,大家都清楚,基本数据类型中的逻辑类型就是逻辑值数据模型和或(∨)、与(∧)、非(┐)三种逻辑运算的统一体;整数类型就是整数值数据模型和加(+)、减(-)、乘(*)、除(div)四种运算的统一体;实型和字符型等也类同。每一种基本类型都连带着一组基本运算。只是由于这些基本数据类型中的数据模型的具体表示和基本运算的具体实现都很规范,都可以通过内置(built-in)而隐蔽起来,使人们看不到它们的封装。许多人已习惯于在算法与程序设计中用基本数据类型名和相关的运算名,而不问其究竟。所以没有意识到抽象数据类型的概念已经孕育在基本数据类型的概念之中。
回到定义算法的顶层和底层的接口,即定义抽象数据类型。根据抽象数据类型的概念,对抽象数据类型进行定义就是约定抽象数据类型的名字,同时,约定在该类型上定义的一组运算的各个运算的名字,明确各个运算分别要有多少个参数,这些参数的含义和顺序,以及运算的功能。一旦定义清楚,算法的顶层就可以像引用基本数据类型那样,十分简便地引用抽象数据类型;同时,算法的底层就有了设计的依据和目标。顶层和底层都与抽象数据类型的定义打交道。顶层运算和底层运算没有直接的联系。因此,只要严格按照定义办,顶层算法的设计和底层算法的设计就可以互相独立,互不影响,实现对它们的隔离,达到抽象的目的。
在定义了抽象数据类型之后,算法底层的设计任务就可以明确为:
- 赋每一个抽象数据类型名予具体的构造数据类型,或者说,赋每一个抽象数据类型名予具体的数据结构;
- 赋每一个抽象数据类型上的每个运算名予具体的运算内容,或者说,赋予具体的过程或函数。
因此,落实下来,算法底层的设计就是数据结构的设计和过程与函数的设计。用高级语言表达,就是构造数据类型的定义和过程与函数的说明。
不言而喻,由于实际问题千奇百怪,数据模型千姿百态,问题求解的算法千变万化,抽象数据类型的设计和实现不可能像基本数据类型那样可以规范、内置、一劳永逸。它要求算法设计和程序设计人员因时因地制宜,自行筹划,目标是使抽象数据类型对外的整体效率尽可能地高。
下面用一个例子来说明,对于一个具体的问题,抽象数据类型是如何定义的。
考虑拓扑排序问题:已知一个集合S={a1,a2, ... ,am},S上已规定了一个部分序<。要求给出S的一个线性序{a1',a2', ... ,am'},即S的一个重排,使得对于任意的1<=j<k<=m,不得有ak'<aj'。这里所谓S上的部分序<,是指S上的一种序关系,它对于S中的任意元素x,y和z,具有如下三个性质:
- 不得有x<x;(反自反性)
- 若x<y,则不得有y<x;(反对称性)
- 若x<y,,且y<z,则x<z;(传递性)。
其中x<y读作x先于y,或等价地读作x是y的前驱,或y是x是后继。
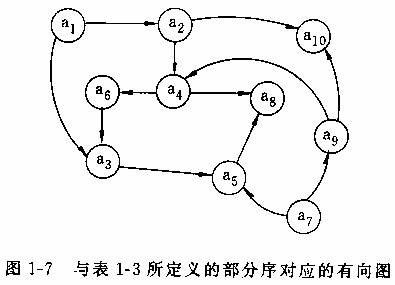
由于已知的S上的部分序<可以用一个有向图G来表示,而要求的S的线性序可以用一个队列Q来表示,所以问题的数据模型包括一类有向图和一类队列。我们将其分别取名为Digraph和Queue。其中G=G(V,E)是Digraph中的一个有向图,结点集V=S,有向边集E是由<决定的S的元素间的有向连线的全体;Q=S={a1,a2, ... ,am}是Queue中的一个队列。在G中,ai和aj之间有一条起于ai止于aj的有向连线的充分必要条件是ai<aj。具体地说,比如S={a1,a2, ... ,a10},而<如表1-3所示,则G(V,E)如图1-7,而Q={a7,a9,a1,a2,a4,a6,a3,a5,a8,a10}。这个Q只是问题的一个解。显然问题的解不唯一,容易举出Q'={a1,a2,a7,a9,a10,a4,a6,a3,a5,a8}是另一个解。
|
a1<a2
|
|
a2<a4
|
|
a4<a6
|
|
a2<a10
|
|
a4<a8
|
|
a6<a3
|
|
a1<a3
|
|
a3<a5
|
|
a5<a8
|
|
a7<a5
|
|
a7<a9
|
|
a9<a4
|
|
a9<a10
|
表1-3 S={a1,a2,...,a10}中的部分序
在数据模型Digraph和Queue的基础上,容易拟定出算法高层的宏观运算步骤,我们称之为算法的主干部分,并用非形式的自然语言表述如下:
1.φ->Q;
2.检测G。
(1)当G≠φ时;
①在G中出任意一个无前驱的结点,记为a;
②将a加到Q的末尾;
③在G中删去结点a以及以a为起点的所有有向边;
④转向2。
(2)当C=φ时,算法结束,问题的解在Q中。
用高级语言中的控制结构语句成分,替换上述主干算法中自然语言的控制转移术语,则主干算法可用自然语言和高级语言的混合语言改述如下:
φ->Q;
while G≠φ do
begin
a:=G中任意一个无前驱的顶点;
将a加到Q的末尾; 从G中删去结点a以及以a为起点的所有有向边;
end;我们看到,其中那些还未能用高级语言表达的语句或语句成分,正是算法需要定义在数据 模型Digraph和Queue上的运算。现分别将它们列出。
对于Digraph中的G:
- 检测G是否非空图;
- 在G中找任意一个无前驱的结点;
- 在G中删去一个无前驱的结点,以及以该结点为起点的所有有向边。
对于Queue中的Q:
- 初始化Q为空队列;
- 将一个结点加到Q的末尾。
如果还考虑到已知G的初始状态如何由输入形成和Q的结果状态的输出,那么,对于Digraph和Queue还需要补充定义若干有关的运算。为了简单,这里从略。
由于高级语言为抽象数据类型的定义提供了很好的环境和工具,再复杂的数据模型都可 以通过构造数据类型来表达,再复杂的运算都可以借助过程或函数来描述。因此,上述由数据模型和数据模型上定义的运算综合起来的抽象数据类型很容易用高级语言来定义。
对于抽象数据类型mgraph,定义如下三个运算:
- (l)function G_empty(G:Digraph):boolean;
- {检测图G是否非空。如果G=φ,则函数返回true,否则返回false}
- (2)function G_front(G:Digraph):nodetype;
- {在有向图G中找一个无前驱的结点。nodetype是结点类型名,它有待用户定义,下同}
- (3)Procedure delete_G_front(var G:Digraph;a:nodetype);
- {在G中删去结点a以及以a为起点的所有有向边}
对抽象数据类型Queue,定义如下两个运算:
- (l)Procedure init_Q(var Q:Queue); {初始化队列Q为空队列}
- (2)Procedure add_Q_rear(a:nodetype;var Q:Queue) {将结点a加到队列Q的末尾}
这样,我们便定义了ADT Digraph和ADT Queue。
有了抽象数据类型Digraph和Queue的上述定义,拓扑排序问题的主干算法即可完全由高级语言表达成主程序。
Program topsort(input,ouput);
type
nodetype=…
Digraph=…
Queue=…
Function G_empty(G:Digraph):boolean;
...
Function G_front(G:Dlgraph):nodetype;
...
Procedure delete_G_front(var G:Digraph;a:nodetype);
...
Procedure init_Q(var Q:Queue);
...
Procedure add_Q_rear(a:nodetype;var Q:Queue);
...
var
a:nodetype;
G:Digraph;
Q:Queue;
begin
… {输入并形成G的初始状态即拓扑排序前的状态}
init_Q(Q);
while not G_empty(G) do
begin
a:=G_front(G);
add_Q_rear(a,Q);
delete_G_front(G,a);
end;
…
{输出Q中的结果}
end;为了简明,我们在其中略去了输入、拓扑排序前G的状态的形成和结果输出三个部分。至于构造数据类型nodetype,Digraph和Queue的表示,函数G_empty,G_front,过程delete_G_front,init_Q和add_Q_rear等的实现,则留待算法的底层设计去完成。需要指出的是,nodetype通常用记录表示,而Digraph和Queue都有多种表示方式。因而G_empty,G_front,delete_G_front,init_Q和add_Q_rear也有多种的实现方式。
但是,只要抽象数据类型Digraph和Queue的定义不变,不管上述构造数据类型的表示和过程与函数的实现如何改变,主程序的表达都不会改变;反过来,不管主程序在哪里调用抽象数据类型上的函数或过程,上述构造数据类型的表示和过程与函数的实现都不必改变。算法顶层的设计与底层的设计之间的这种独立性,显然得益于抽象数据类型的引人。而这种独立性给算法和程序设计带来了许多好处。